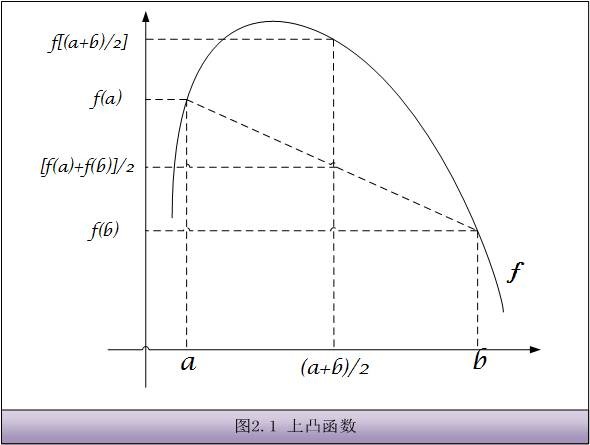
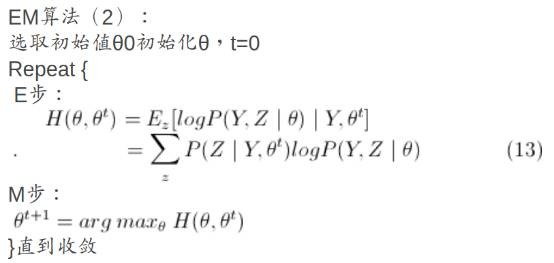1. 凸函数
- 上凸函数
- f[(a+b)/2] ≥ [f(a)+f(b)]/2
- 当a≠b时
- f[(a+b)/2] > [f(a)+f(b)]/2
成立,那么称f(x)为严格的上凸函数,等号成立的条件当且仅当a=b,下凸函数与其类似。
- f[(a+b)/2] > [f(a)+f(b)]/2
2. Jensen不等式
- 如果f是上凸函数,X是随机变量,那么
- f(E[X]) ≥ E[f(X)].
- 如果f是严格上凸函数,那么
- E[f(X)] = f(E[X])
- 当且仅当p(X=E[X]),也就是说X是常量。
3. EM算法
3.1. Problem Definition
考虑一个参数估计问题,现有共n个训练样本,需有多个参数θ去拟合数据(高斯混合模型),那么这个log似然函数是
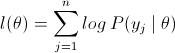
由于Θ中多个参数的某种关系,导致上面的log似然函数无法直接或梯度下降法求最大值时的Θ值。引入隐变量z,并使用Jensen不等式得到下界
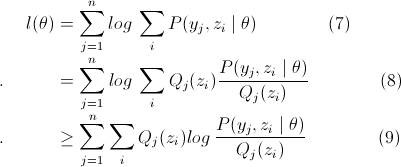
(9)式紧下界为等号成立时,即随机变量

为常数。又因为
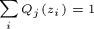
有

所以(9)成立的条件是
- Q(zi)=P(zi|yi, Θ)
- 即后验概率。
3.2. Algorithm Step
- E步骤 已知(初始化)Θ和样本数据yi,计算Q(zi)。
- M步骤 利用Q(zi)简化(9)中的多项式,从而可用梯度下降求偏导更新Θ值。
- E步骤 根据Θ计算Q(zi).
- M步骤 根据Q(zi)更新Θ.
- …
- 迭代直至收敛。